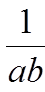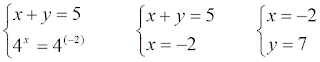воскресенье, 31 июля 2016 г.

ЗНО з математики № 26

На рисунку зображено квадрат

ABCD, сторона якого дорівнює

15. На сторонах

ADі

BC квадрата вибрано точки

K і

M так, що

AK=4, MC=3.

1. Визначте відстань між серединами відрізків

AB і

KM.

2. Обчисліть довжину відрізка

KM.

Відповідь надайте у вигляді двох чисел, розділених крапкою з комою.

ЗНО з математики № 25

У бібліотеці є лише підручники, словники, довідники та художня література. Відсотковий розподіл кількості цих книг у бібліотеці відображено на діаграмі.

1. Визначте загальну кількість книг у цій бібліотеці, якщо кількість підручників дорівнює

72.

2. Скільки потрібно придбати додатково підручників, щоб отримана після цього їх сумарна кількість відносилася до кількості довідників як

4 : 1.

Відповідь надайте у вигляді двох чисел, розділених крапкою з комою.

суббота, 30 июля 2016 г.

В даному блозі будемо готуватись до здачі ЗНО,ДПА, розв'язуючи вправи які були на даних іспитах в різних роках. Оскільки по більш складним завданням знімаю відео, то тут будемо розглядати простенькі вправи.

24. Установіть відповідність між геометричним тілом (1—4) та площею його повної поверхні (А—Д).

Геометричне тіло	Площа повної поверхні
1. конус із радіусом основи 3 та твірною 5	А. 18π
2. циліндр із радіусом основи 3 та висотою 4	Б. 24π
3. куля радіуса 2√3	В. 36π
4. куб із ребром √(3π)	Г. 42π
	Д. 48π

Розв'язання

1.Конус: S=πrl+πr²=π3*5+π*9=(15+9)π=24π
1-Б.

2. Циліндр: S=2πrh+2πr²=2π*12+18π=42π.
2-Г.

3. Куля: S=4πr²=4π*12=48π
3-Д.

4. Куб: S=6a²=6*3π=18π
4-B.

Відповідь: 1-Б; 2-Г; 3-Д; 4-A.

четверг, 28 июля 2016 г.

ЗНО з математики № 23

23. На рисунку зображено коло з центром у точці O, радіус якого дорівнює 6. Хорду BC видно з центра кола під кутом 60^∘, BK — діаметр. Через точку A до кола проведено дотичну AB, причому AO=2AB. Установіть відповідність між відрізком (1—4) та його довжиною (А—Д).

Відрізок	довжина відрізка
1. BK	А. 2√3
2. AB	Б. 6
3. BС	В. 6√3
4. СК	Г. 3√3
	Д. 12

Розв'язання

1. Оскільки радіус дорівнює 6, а ВК - діаметр, то ВК=12.
1-д.

2. Трикутник АВО прямокутний (кут B=90^o),і за умовою AO=2AB, то cosA=0,5.А звідси слідує, що кут А=60 ^o. AB=OB* ctg A=6*√3/3=2√3.
2-A.

3. Трикутник ОВС рівносторонній, ОВ=ОС як радіуси, і кути при основі по 60 градусів.Тому ВС=ОВ=6.
3-Б.

4. ОС=ОК=6,як радіуси, кут СОК=120^o, так як суміжний з кутом 60 ^o Кути ОСК=ОКС рівні і дорівнюють 30 ^o.Трикутник ВСК прямокутний, кут С=90 ^o(60+30=90),кут ВКС=30. СК=ВК*cos 30=12*√3/2=6√3.
4-B.

Відповідь: 1-Д; 2-А; 3-Б; 4-В.

среда, 27 июля 2016 г.

ЗНО з математики № 22

22. Установіть відповідність між числовим виразом (1—4) та його значенням (А—Д), якщо a=25/4.

Розв'яання

1-Г

2-Б.

3.

3-В.

4.

4-А.

Відповідь: 1-Г; 2-Б; 3-В; 4-А.

понедельник, 25 июля 2016 г.

ЗНО з математики № 21

21. На рисунках (1—5) зображено графіки функцій, визначених на відрізку [−3; 3].

До кожного запитання (1—4) доберіть правильну відповідь (А—Д).

Запитання

1. На якому рисунку зображено графік парної функції?

2. На якому рисунку зображено графік функції, що проходить через точку (1; 0)?

3. На якому рисунку зображено графік функції, що зростає на відрізку [−2; 3]?

4. На якому рисунку зображено графік функції, що має дві спільні точки з графіком функції y=log_1/3x?

Відповідь

А. рис. 1

Б. рис. 2

В. рис. 3

Г. рис. 4

Д. рис. 5

1. На якому рисунку зображено графік парної функції?Графік парної функції симетричний відносно осі ОУ. Задовольняє рис. 2. 1-Б.

2. На якому рисунку зображено графік функції, що проходить через точку (1; 0)? По графікам видно, що на рис. 1. 2-А.

3. На якому рисунку зображено графік функції, що зростає на відрізку [−2; 3]? Функція зростає, якщо більшому значенню аргумента відповідає більше значення функції.Зрозуміло, щол це рис. 3. 3-В.

4. На якому рисунку зображено графік функції, що має дві спільні точки з графіком функції y=log_1/3x?

з графіка видно, що це рис. 4. 4-Г.

Відповідь:
1-Б

2-А

3-В

4-Г

воскресенье, 24 июля 2016 г.

ЗНО з математики № 20

20. Розв'яжіть рівняння

А. ±π/6+2πn,n∈Z

Б. π/3+πn,n∈Z

В. π/6+2πn,n∈Z

Г. π/9+πn/3,n∈Z

Д. π/6+πn,n∈Z

x=π/6+πn,n∈Z

Відповідь: Д. π/6+πn,n∈Z

суббота, 23 июля 2016 г.

ЗНО з математики № 19

19. Використовуючи формулу Ньютона — Лейбніца, обчисліть

А. 42

Б. 22

В. 18

Г. 14

Д. 12

Відповідь: Г. 14

ЗНО з математики № 18

18. Розв'яжіть нерівність log₃ x < − 1.

А. (0; 1/3). 0

Б. (−∞; 1/3)

В. (−1/3; 0)

Г. (−∞; −3)

Д. (1/3; +∞)

Шукаємо ОДЗ: х>0;

Перепишемо наступним чином:

log₃ x < log₃1/3.

Оскільки 3>1 функція логарифмічна зростаюча, тому:

x < 1/3;

Враховуючи ОДЗ отримаємо

0 < x < 1/3;

xє(0;1/3).

Відповідь: A. (0; 1/3)

четверг, 21 июля 2016 г.

ЗНО з математики № 17

17. Обчисліть значення виразу 4sin²α, якщо 4cos²α=1.

A. 0

Б. 1/4

В. 3/4

Г. 3

Д. 4

За відомою формулою:

sin²α+cos²α=1;

Домножимо праву і ліву частину на 4;

4sin²α+4cos²α=4;

4sin²α=4-4cos²α;

4sin²α=4-1=3;

4sin²α=3.

Відповідь: Г. 3

среда, 20 июля 2016 г.

ЗНО з математики № 16

16. Визначте об'єм правильної трикутної призми, бічні грані якої є квадратами, а периметр основи дорівнює 12.

A. 16√3

Б. 64

В.48

Г. 64√3

Д. 576

Периметр основи 12. В основі лежить правильний трикутник,тому його сторона 12:3=4. За умовою, що бічні грані якої є квадратами, то H=4.

V=S_осн*H=4*S_осн.

В основі лежить правильний трикутник, (див. нижче)

Відповідь: А

понедельник, 18 июля 2016 г.

ЗНО з математики № 15

15. Яка з наведених парабол може бути графіком функції y=x²+px+q, якщо рівняння x²+px+q=0 не має дійсних коренів?

Якщо рівняння не має дійсних коренів, то графік не перетинає вісь ох, оскільки а=1>0, то вітки параболи направлені вгору. графік В може бути графіком заданої функції

Відповідь: В

ЗНО з математики № 14

14.

A.3

Б. 3,3

В. 0,25

Г. 4

Д.

Відповідь: A.3

воскресенье, 17 июля 2016 г.

ЗНО з математики № 13

13. Екрани телевізорів, зображених на рис. 1 і 2, мають форму прямокутників, відповідні сторони яких пропорційні. Діагоналі екранів цих телевізорів дорівнюють відповідно 32 дюйми і 48 дюймів. Визначте, у скільки разів площа екрана телевізора, зображеного на рис. 2, більша за площу екрана телевізора, зображеного на рис. 1.

A.в 1,5 раза

Б. у 2,25 раза

В.у 2,56 раза

Г.у 4 рази

Д. у 16 разів

Прямокутники подібні і їх площі відносяться як квадрати відповідних сторін, тобто 48²/32²=2304/1024=2,25

Відповідь: у 2,25 раза

суббота, 16 июля 2016 г.

ЗНО з математики № 12

12. Задано арифметичну прогресію (a_n), у якій різниця d=0,5, п'ятнадцятий член a₁₅=12. Визначте перший член прогресії a₁.

A. 4,5

Б. 5

В.6

Г. 12,5

Д. 24

a₁₅=a₁+14d;
12=a₁+14*0,5
12=a₁+7
5=a₁
a₁=5

Відповідь: Б.

пятница, 15 июля 2016 г.

ЗНО з математики № 11

11. Спростити

Б.

В.

Г.

Д. 0

Відповідь: А.

ЗНО з математики № 10

10. Прямі a та b мимобіжні. Які з наведених тверджень є правильними?
I. Прямі a та b перетинаються.

II. Прямі a та b лежать в одній площині.

III. Існує пряма, паралельна прямій a, що перетинає пряму b.

A.лише I

Б. лише II

В. лише III

Г. лише I та II

Д.I, II та III

Дві прямі, що не належать одній площині називають мимобіжними.Тому вони не можуть перетинатись, так як в противному випадку через них можна було б провести площину(не І).І не ІІ(суперечить означенню мимобіжних прямих). На прямій b можна взяти будь-яку точку і через неї провести пряму паралельну прямій а (ІІІ вірно). Тому правильна відповідь лише ІІІ, а це В.

Відповідь: В. лише III

четверг, 14 июля 2016 г.

ЗНО з математики № 6

6.Розв'яжіть систему рівнянь .
Якщо (x0; y0) — розв'язок цієї системи, то x0⋅y0=

A. -36

Б. -14

В. -6

Г. 4

Д. 6

x0⋅y0=-7*2=-14

Відповідь: Б. −14

среда, 13 июля 2016 г.

ЗНО з математики № 9

9.Якому проміжку належить число

A.[0; 1)

Б. [1; 2)

В. [2; 3)

Г. [3; 4)

Д.[4; +∞)

Аналізуємо,

Видно, що наше значення належить проміжку В.[2; 3)

Відповідь: В. [2; 3)

вторник, 12 июля 2016 г.

ЗНО з математики № 8

8.Якому значенню серед наведених може дорівнювати довжина сторони AC трикутника ABC, якщо AB=3 см, BC=10 см?

A. 3 см

Б. 5 см

В. 7 см

Г. 11 см

Д. 15 см

Подумаємо,

А. 3+3<10 суперечить нерівності трикутника

Б. 5+3<10 суперечить нерівності трикутника

В. 7+3=10 суперечить нерівності трикутника

Г. 11 см 3 см і 10 см задовольняє 11+3>10 11+10>3 3+10>11

Перевіримо, на всяк випадок Д.

Д. 3+10<15 суперечить нерівності трикутника

Відповідь: Г. 11 см

понедельник, 11 июля 2016 г.

ЗНО з математики № 7

7.На рисунку жирними точками позначено річні мінімуми площі поверхні арктичного льоду, що спостерігалися з 2004 р. до 2014 р. (для наочності точки з'єднано відрізками). По горизонталі відмічено роки, а по вертикалі — площу поверхні льоду (у млн км²). Користуючись наведеною інформацією, визначте із зазначеного періоду рік, у якому величина річного мінімуму площі поверхні льоду змінилась найбільше порівняно з попереднім роком.

A. 2006 р.

Б. 2007 р.

В. 2009 р.

Г. 2012 р.

Д. 2013 р.

Дивлячись на графік, знайдемо зміни площ поверхні льоду:

2006 р.: 5,7-5,2= 0,5

2007 р.: 5,7-4,2= 1,5

2009 р.: 5,1-4,6= 0,5

2012 р.: 4,2-3,4= 0,8

2013 р.: 5,1-3,4= 1,7 і Це найбільша зміна величини мінімуму площі поверхні арктичного льоду за рік в період з 2004 р. по 2014 р.

Відповідь: Д. 2013 р.

ЗНО з математики № 5

5.У прямокутній декартовій системі координат у просторі на осі z вибрано точку M (див. рисунок). Серед наведених варіантів укажіть можливі координати цієї точки.

A. (1; 0; 0)

Б.(1; 1; 0)

В.(0; 1; 0)

Г.(0; 0;−1)

Д. (0; 0; 1)

Оскільки точка М лежить на осі z, то х=0 та у=0, і вище точки О(початку координат), то z>0, тому правильна відповідь, яка відповідає нашим вимогам Д(0; 0; 1).

Відповідь: Д(0; 0; 1)

воскресенье, 10 июля 2016 г.

ЗНО з математики № 4

4. Укажіть число, що є розв'язком нерівності

A. -2

Б. 0

В.2

Г. 4

Д. 9

Саме просте взяти і підставити кожен розв'язок у нашу нерівність, можна звісно розв'язати нерівність, а потім написати відповідь.

A. x=-2 5/(-5)=-1<1, не задовольняє нашу нерівність.

Б. х=0, 5/(-3)=-5/3<1,не задовольняє нашу нерівність теж.

В. х=2, 5/(-1)=-5<1, те ж, що і А. і Б.

Г. х=4 5/1=5>1, що і є розв'язком

На всяк випадок перевіримо і Д. х=9, 5/6<1, те саме, що і А, Б,В.

Відповідь: Г. х=4.

ЗНО. завдання № 3.

3. Графіком однієї з наведених функцій є пряма. Укажіть цю функцію.

A. y=2^x

Б. y=x²-2x

В. y=cos(2x)

Г. $y= \frac{2}{x}$

Д. y=2x

Як ми знаємо, рівняння прямої y=kx+b,де k,b- дійсні числа. Бачимо, що під цю формулу підпадає варіант y=2x, де k=2,b=0.

Відповідь: Д.y=2x

суббота, 9 июля 2016 г.

ЗНО завдання № 2.

2. На рисунку прямі m і n, що перетинаються. Визначте градусну міру кута γ, якщо α+β=50^o

A. 130 ^o

Б. 140 ^o

В. 145 ^o

Г. 155 ^o

Д. 310 ^o

Оскільки кути вертикальні, то α=β=25^o. Так як γ і α суміжні, їх сума дорівнює 180 ^o Тоді γ=180-25=155 ^o.

Відповідь: Г. 155 ^o

завдання № 1. ЗНО

**1. 0,4x²*5x³=**

A. 2x⁵
Б. 20x⁵
В. 2x⁶
Г. 0,2x⁵
Д. 0,2x⁶
Розв'язання

помножимо числа та букви:

0,4x²*5x³=0,4*5x ² * x³=2x⁵

Відповідь. А.

Математика

воскресенье, 31 июля 2016 г.

суббота, 30 июля 2016 г.

24. Установіть відповідність між геометричним тілом (1—4) та площею його повної поверхні (А—Д).

Розв'язання

Відповідь: 1-Б; 2-Г; 3-Д; 4-A.

четверг, 28 июля 2016 г.

Розв'язання

Відповідь: 1-Д; 2-А; 3-Б; 4-В.

среда, 27 июля 2016 г.

22. Установіть відповідність між числовим виразом (1—4) та його значенням (А—Д), якщо a=25/4.

Розв'яання

Відповідь: 1-Г; 2-Б; 3-В; 4-А.

понедельник, 25 июля 2016 г.

21. На рисунках (1—5) зображено графіки функцій, визначених на відрізку [−3; 3].

До кожного запитання (1—4) доберіть правильну відповідь (А—Д).

Запитання

Відповідь

Відповідь: 1-Б 2-А 3-В 4-Г

воскресенье, 24 июля 2016 г.

20. Розв'яжіть рівняння

А. ±π/6+2πn,n∈Z

Б. π/3+πn,n∈Z

В. π/6+2πn,n∈Z

Г. π/9+πn/3,n∈Z

Д. π/6+πn,n∈Z

Відповідь: Д. π/6+πn,n∈Z

суббота, 23 июля 2016 г.

19. Використовуючи формулу Ньютона — Лейбніца, обчисліть

А. 42

Б. 22

В. 18

Г. 14

Д. 12

Відповідь: Г. 14

18. Розв'яжіть нерівність log3 x < − 1.

А. (0; 1/3). 0

Б. (−∞; 1/3)

В. (−1/3; 0)

Г. (−∞; −3)

Д. (1/3; +∞)

xє(0;1/3).

Відповідь: A. (0; 1/3)

четверг, 21 июля 2016 г.

17. Обчисліть значення виразу 4sin2α, якщо 4cos2α=1.

A. 0

Б. 1/4

В. 3/4

Г. 3

Д. 4

Відповідь: Г. 3

среда, 20 июля 2016 г.

16. Визначте об'єм правильної трикутної призми, бічні грані якої є квадратами, а периметр основи дорівнює 12.

A. 16√3

Б. 64

В.48

Г. 64√3

Д. 576

Відповідь: А

понедельник, 18 июля 2016 г.

15. Яка з наведених парабол може бути графіком функції y=x2+px+q, якщо рівняння x2+px+q=0 не має дійсних коренів?

Відповідь: В

14.

A.3

Б. 3,3

В. 0,25

Г. 4

Д.

Відповідь: A.3

воскресенье, 17 июля 2016 г.

A.в 1,5 раза

Б. у 2,25 раза

В.у 2,56 раза

Г.у 4 рази

Д. у 16 разів

Відповідь: у 2,25 раза

суббота, 16 июля 2016 г.

12. Задано арифметичну прогресію (an), у якій різниця d=0,5, п'ятнадцятий член a15=12. Визначте перший член прогресії a1.

A. 4,5

Б. 5

воскресенье, 31 июля 2016 г.

суббота, 30 июля 2016 г.

четверг, 28 июля 2016 г.

среда, 27 июля 2016 г.

понедельник, 25 июля 2016 г.

Відповідь:
1-Б

2-А

3-В

4-Г

воскресенье, 24 июля 2016 г.

суббота, 23 июля 2016 г.

18. Розв'яжіть нерівність log₃ x < − 1.

четверг, 21 июля 2016 г.

17. Обчисліть значення виразу 4sin²α, якщо 4cos²α=1.

среда, 20 июля 2016 г.

понедельник, 18 июля 2016 г.

15. Яка з наведених парабол може бути графіком функції y=x²+px+q, якщо рівняння x²+px+q=0 не має дійсних коренів?

воскресенье, 17 июля 2016 г.

суббота, 16 июля 2016 г.

12. Задано арифметичну прогресію (a_n), у якій різниця d=0,5, п'ятнадцятий член a₁₅=12. Визначте перший член прогресії a₁.

пятница, 15 июля 2016 г.

четверг, 14 июля 2016 г.

6.Розв'яжіть систему рівнянь .
Якщо (x0; y0) — розв'язок цієї системи, то x0⋅y0=

среда, 13 июля 2016 г.

вторник, 12 июля 2016 г.

понедельник, 11 июля 2016 г.

воскресенье, 10 июля 2016 г.

суббота, 9 июля 2016 г.

2. На рисунку прямі m і n, що перетинаються. Визначте градусну міру кута γ, якщо α+β=50^o

**1. 0,4x²*5x³=**